Jak przewidzieć czas w maratonie na podstawie czasu z półmaratonu

Szczegóły

Kategoria: różne

Utworzono: niedziela, 01, wrzesień 2013 20:15

Tadeusz Kielak

 

Startując w maratonie powinno się znać mniej więcej czas w jakim się go ukończy. Nie jest to dystans, na którym można sobie pozwolić na podejmowanie decyzji o strategii w trakcie jego trwania.

Nierzadko ostatecznym sprawdzianem przed startem w maratonie jest start w półmaratonie w terminie kilka tygodni wcześniejszym.

Przeglądając Internet można natrafić na kilka różnych metod przewidywania czasu w maratonie na podstawie uzyskanego czasu na dystansie o połowę krótszym.

 

1. Metody klasyczne (A i B)

Poniższe dwa wzory pozwalają wyliczyć czas maratonu na najczęściej spotykane sposoby:

1. Czas_maraton = czas_półmaraton * 2 + 5 minut
2. Czas_maraton = czas_półmaraton * 2,11

Spróbujmy zweryfikować trafność tych metod w odniesieniu do amatorskich zawodników uczestniczących w masowych biegach ulicznych.

Wiosną 2013 w Warszawie odbyły się dwa duże biegi uliczne w odstępie około miesiąca – 8 Półmaraton Warszawski 24 marca i Orlen Warsaw Marathon 21 kwietnia. Okazuje się, że aż 1 440 osób ukończyło oba biegi.

Załóżmy, że dla większości z nich półmaraton był sprawdzianem przed maratonem. Osiągnięte przez nich rezultaty będą podstawą do dalszych rozważań. Średni czas 1 440 zawodników w Półmaratonie Warszawskim był równy 1:46:37,8. Jeżeli do tego czasu zastosujemy metody A i B otrzymamy następujące prognozowane czasy ukończenia maratonu:

1. 3:38:15,6
2. 3:44:59,3

Tymczasem rzeczywisty średni czas tych samych 1 440 zawodników w Warsaw Marathon wyniósł 4:03:06,7. Błędy bezwzględne szacowania obu metod były zatem następujące.

1. 24:51,1
2. 18:07,4

W ujęciu względnym błędy obu metod wyniosły:

1. 10,22%
2. 7,45%

Okazuje się zatem, że obie metody szacowania nie mają żadnej wartości praktycznej dla większości biegaczy z uwagi na zbyt dużą rozbieżność pomiędzy czasem uzyskanym a prognozowanym.

2. Metoda C

Poszukajmy zatem innych metod szacowania wyniku w maratonie. Na początek zmodyfikujmy metodę B. Innymi słowy poszukamy lepszego niż 2,11 współczynnika.

Dla każdego z 1 440 biegaczy wyliczmy iloraz czasu uzyskanego maratonie i czasu uzyskanego w półmaratonie. Wartość średnia wyliczonych współczynników jest równa 2,2824. Zatem otrzymujemy kolejną metodę szacowania:

Czas_maraton = czas_półmaraton * 2,2824

Poniższy wykres częstości współczynników w badanej próbce (histogram) pokazuje, że większość skupia się wokół wyznaczonej wartości. W związku z tym możemy stwierdzić, że metoda C pozwala o wiele lepiej przewidzieć czas niż metody A i B. Tym niemniej warto poszukać jeszcze dokładniejszej metody.

 

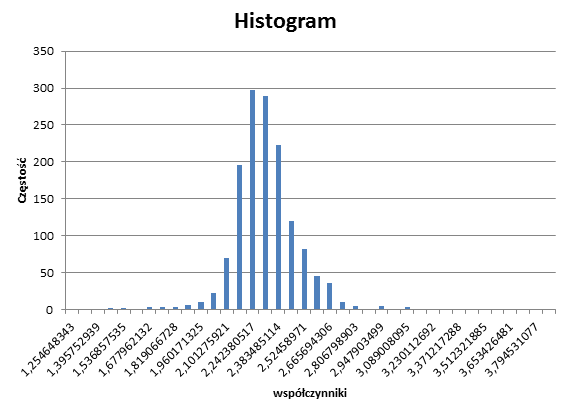
Możemy wyznaczyć oddzielne współczynniki dla określonych podzbiorów zawodników. Poniższa tabela zawiera wyliczone współczynniki dla mężczyzn i dla kobiet. Zauważyć należy jednak, że o ile w przypadku mężczyzn „próbka” jest wystarczająco duża to w przypadku kobiet już tak nie jest . Ponieważ liczba kobiet w badanej próbce jest mniejsza niż 10% ta i wszystkie inne opisane w tym artykule metody, które biorą pod uwagę płeć zawodnika obarczone są dodatkowym błędem.

 

płeć	liczba zawodników	średni współczynnik
K	129	2,249
M	1 311	2,286
	1 440	2,282

 

Wskaźniki wyliczone dla poszczególnych kategorii wiekowych charakteryzują się mniejszą wiarygodnością niż te z poprzedniej tabeli z uwagi na mniejsze próbki. Zauważyć można jednakże pewne prawidłowości. W przypadku kobiet współczynniki są prawie zawsze mniejsze niż u mężczyzn co świadczyć może np. o tym, że profil startujących kobiet bliższy jest profilowi zawodników biegających profesjonalnie. Podobnie łatwo jest zauważyć, że niższe współczynniki charakteryzują biegaczy starszych.

 

kategoria wiekowa	liczba zawodników	średni współczynnik
K20	26	2,265
K30	57	2,256
K40	32	2,247
K50	11	2,193
K60	2	2,118
K70+	1	2,449
M20	190	2,314
M30	532	2,294
M40	410	2,27
M50	143	2,274
M60	34	2,234
M70+	2	2,3
	1440	2,282

Współczynniki wyliczone oddzielnie dla każdego rocznika obarczone są już zbyt dużym błędem statystycznym z uwagi na niewielką liczbę zawodników w poszczególnych grupach.

 

rok urodzenia	liczba zawodników	średni współczynnik
1933	1	2,261
1939	1	2,338
1942	1	2,449
1946	2	2,071
1947	5	2,316
1948	3	2,309
1949	7	2,185
1950	5	2,191
1951	3	2,203
1952	4	2,260
1953	7	2,237
1954	8	2,202
1955	9	2,230
1956	12	2,263
1957	14	2,275
1958	11	2,249
1959	22	2,286
1960	21	2,259
1961	19	2,269
1962	10	2,274
1963	28	2,297
1964	16	2,260
1965	24	2,288
1966	28	2,259
1967	31	2,292
1968	44	2,222
1969	33	2,255
1970	64	2,284
1971	53	2,269
1972	59	2,259
1973	90	2,280
1974	74	2,290
1975	62	2,280
1976	74	2,296
1977	72	2,308
1978	58	2,251
1979	58	2,311
1980	51	2,261
1981	54	2,301
1982	36	2,303
1983	50	2,299
1984	35	2,287
1985	44	2,316
1986	34	2,305
1987	24	2,306
1988	23	2,314
1989	20	2,265
1990	11	2,224
1991	10	2,329
1992	5	2,322
1993	5	2,295
1994	5	2,716
	1440	2,282

 

Dotychczas zaprezentowane metody zostały opracowane przy pomocy prostych reguł i programu MS Excell.

Kolejne metody opisane metody wykorzystują nieco więcej statystyki.

 

3. Metoda D

Przyjmijmy teraz, że (tak samo jak w metodzie A) modelem zależności pomiędzy rezultatami osiągniętymi w półmaratonie i w maratonie jest funkcja liniowa y=ax+b, gdzie x jest czasem osiągniętym w półmaratonie a y prognozowanym czasem w maratonie. Do wyznaczenia poszukiwanych parametrów funkcji liniowej (a i b) wykorzystamy program R i nakładkę graficzną RStudio.

Na początek wrzucamy wszystkie 1 440 par wartości wyników w obu biegach (wyrażone w sekundach).

Poniższy wykres przedstawia wszystkie 1 440 pary wyników (czerwone kółka) oraz prostą (kolor zielony), reprezentującą poszukiwaną zależność liniową.

Prosta ta została wyznaczona metodą regresji liniowej przy użyciu metody najmniejszych kwadratów.

Wyliczone przez program R współczynniki są równe 2,081 i 1273,2. Poszukiwana funkcja ma zatem postać y=2,081x+1273,2.

Podobnie jak w przypadku poszukiwania wartości średnich współczynników możemy wykorzystać program R i metodę najmniejszych kwadratów dla podzbiorów danych. I tak dla kobiet otrzymujemy poniższy wykres:

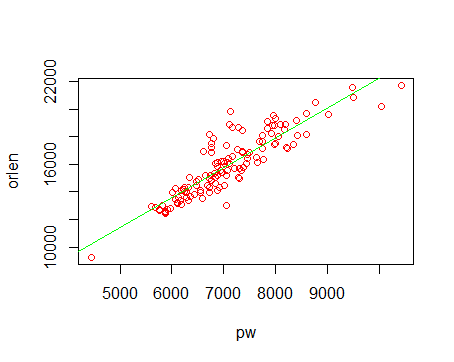
Poszukiwana funkcja dla kobiet przyjmuje postać y=2,16x+632,3.

W przypadku podzbioru mężczyzn otrzymujemy poniższy wykres.

Poszukiwana funkcja dla mężczyzn przyjmuje postać y=2,08x+1285,9.

 

4. Metoda E

 

Spróbujmy teraz spojrzeć na problem jeszcze z innej strony. Zbadajmy mianowicie zależność ilorazu uzyskanych czasów w zawodach od wieku zawodników.Przyjmijmy na początek, że zależność ta jest liniowa. Poszukujemy parametrów funkcji liniowej postaci y=ax+b.

Wrzućmy zatem do programu R listę postaci (wiek zawodnika, iloraz czasów osiągniętych w maratonie i półmaratonie).

Po zastosowaniu metody regresji liniowej i metody najmniejszych kwadratów

Wyliczony wzór na poszukiwany współczynnik ma zatem postać następującą:

wsp=-0,0017848*wiek+2,35191
Pełny wzór na czas w maratonie wygląda zatem tak:

czas_maraton=(-0,0017848*wiek+2,35191)*czas_półmaraton

Dla podzbioru kobiet otrzymujemy wykres:

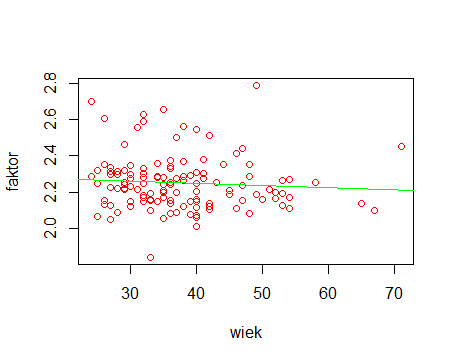
i wzór:
czas_maraton=(-0,001186*wiek+2,29379)*czas_półmaraton


Dla podzbioru mężczyzn

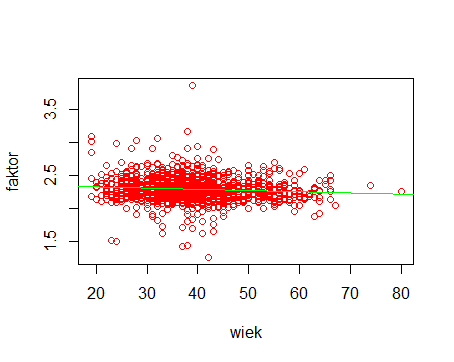
i wzór:
czas_maraton=(-0,00191236*wiek+2,3604)*czas_półmaraton

5. Porównanie metod

Poniższa tabela zawiera zestawienie dyskutowanych metod szacowania czasu w maratonie. Należy ją czytać w następujący sposób:

Górny wiersz zawiera oczekiwaną dokładność szacowania.

Każdy następny wiersz zawiera prawdopodobieństwo poprawnego oszacowania wyniku dla konkretnych oczekiwanych dokładności.

metoda	1%	2%	3%	4%	5%	6%	7%	8%	9%	10%
A	1,88%	4,31%	7,50%	11,81%	16,74%	22,08%	29,65%	36,94%	43,61%	51,32%
B	6,53%	12,08%	18,75%	25,90%	33,75%	40,83%	47,99%	56,04%	62,50%	69,44%
C - jeden współczynnik	13,40%	25,56%	37,92%	48,54%	58,06%	66,74%	72,78%	78,26%	83,13%	87,64%
C wg płci	13,40%	25,69%	37,92%	48,61%	59,17%	67,43%	73,26%	78,54%	83,33%	87,85%
C wg wieku	13,89%	27,78%	40,21%	50,69%	59,51%	67,29%	73,40%	79,03%	83,82%	87,71%
D - jeden współczynnik	12,92%	24,44%	36,94%	47,15%	55,90%	64,31%	71,39%	77,36%	81,18%	86,04%
D wg płci	12,57%	24,31%	37,01%	46,74%	55,97%	64,65%	71,60%	77,43%	81,04%	85,97%
E - jeden współczynnik	14,58%	25,49%	38,19%	49,31%	59,03%	66,25%	73,06%	78,68%	83,47%	87,36%
E wg płci	14,03%	26,53%	38,75%	48,89%	58,96%	67,57%	73,68%	79,10%	83,47%	87,50%

Jeżeli na przykład interesuje nas oszacowanie wyniku w maratonie z dokładnością 3% to przy zastosowaniu np. metody B prawdopodobieństwo sukcesu jest równe 18,74%.

Na zielono zaznaczono rekomendowane metody szacowania wyniku w sytuacji, kiedy oczekujemy najdokładniejszych przybliżeń. Zarówno w przypadku szacowania z dokładnością do 1 jak do 2% powinniśmy zastosować jeden z wariantów metody E.

Tabela potwierdza w szczczególnosci tezę mówiącą, o tym, że metody A i B nie nadają się do szacowania wyniku w przypadku statystycznego biegacza.

 

6. Elita

Skoro metody A i B są takie słabe to skąd się w ogóle wzięły. Rozważmy rekordy życiowe grupy czołowych biegaczy i biegaczek z Kenii i z Etiopii. W kolumnach A i B znajdują się wyliczone metodami A i B przewidywane czasy w maratonie na podstawie rekordów życiowych w półmaratonie. Widać jasno, że obie metody w przypadku elity biegaczy zaczynają działać.

	HM	M	A	błąd	B	błąd
Wilson Kipsang Kiprotich	00:58:59	02:03:42	02:02:58	-0,59%	02:04:27	-0,61%
Tsegaye Kebede	00:59:35	02:04:38	02:04:10	-0,37%	02:05:43	-0,87%
Geoffrey Mutai	00:58:58	02:04:15	02:02:56	-1,06%	02:04:25	-0,14%
Dennis Kimetto	00:59:14	02:04:16	02:03:28	-0,64%	02:04:59	-0,58%
Ayele Abshiro	00:59:42	02:04:23	02:04:24	0,01%	02:05:58	-1,27%
Yemane Adhane	01:01:37	02:04:48	02:08:14	2,75%	02:10:01	-4,18%
Feyisa Lilesa	00:59:22	02:04:52	02:03:44	-0,91%	02:05:16	-0,32%
Mary Keitany	01:05:50	02:18:37	02:16:40	-1,41%	02:18:54	-0,21%
Tiki Gelana	01:07:48	02:18:58	02:20:36	1,18%	02:23:03	-2,94%
Priscah Jeptoo	01:06:11	02:20:14	02:17:22	-2,04%	02:19:39	0,42%
Aselefech Mergia	01:07:21	02:19:31	02:19:42	0,13%	02:22:07	-1,86%
Edna Kiplagat	01:07:41	02:19:50	02:20:22	0,38%	02:22:49	-2,13%
Aberu Kebede	01:07:39	02:20:30	02:20:18	-0,14%	02:22:44	-1,60%
Sharon Cherop	01:07:08	02:22:39	02:19:16	-2,37%	02:21:39	0,70%
Lydia Cheromei	01:07:26	02:21:30	02:19:52	-1,15%	02:22:17	-0,55%

 

7. Podsumowanie

 

Oprócz, klasycznych metod A i B wprowadziliśmy trzy dodatkowe metody C, D i E (z podwariantami). Założeniem "nowych" metod jest przeświadczenie o reprezentatywności wyników z Półmaratonu Warszawskiego i Orlen Marathonu.

Ponieważ, dotychczas odbyła się dopiero jedna edycja maratonu Orlenu niemożliwe było zbadanie powtarzalności metod.

Weryfikacja tego rodzaju zostanie przeprowadzona wiosną 2014 (o ile oczywiście obie imprezy się odbędą).

Chociaż najdokładniejsza wydaje się metoda E to łatwiejsza do samodzielnego wykorzystania jest metoda C (Czas_maraton = czas_półmaraton * 2,2824).
Wystarczy bowiem zapamiętać mnożnik równy 2,2824.

 

Biegacze dysponujący wieloma rezultatami uzyskiwanymi w różnych sezonach i okolicznościach mogą przy pomocy kalkulatora sprawdzić, która metoda jest najbardziej optymalna w ich przypadku.

_{Arkusz z danymi źródłowymi i zestawieniem trafności metod.}